SECRET CONVE.RSA.TIONS (Crypto Writeup) -- Hacky Holidays - Unlock The City! 2022

July 27, 2022 | 6 Minute Read

The third edition of the famous Deloitte Hacky Holidays CTF competition start July 8 and finish July 26, 2022. This Year it's "Unlock the city!", It was 18 days of challenges, divided in 4 districts, 33 challenges in total, where 1242 active players tried to unlock the city. Very well elaborated with an excellent platform and well thought out challengess. We chose this CRYPTO challenge for the writeup because it's a very good practical example that no matter how many resources you have, a BAD implementation of an algorithm will always be a persistent threat to you.

Challenge Description:

File to download (source here)

The begginig of the Investigation

We begin our analysis with the letter left by the AI. We open it, and this is its content:

┌──(leonuz㉿sniperhack)-[~/Downloads/hackazon/rsa]
└─$ cat message.txt
N = 5261933844650100908430030083398098838688018147149529533465444719385566864605781576487305356717074882505882701585297765789323726258356035692769897420620858774763694117634408028918270394852404169072671551096321238430993811080749636806153881798472848720411673994908247486124703888115308603904735959457057925225503197625820670522050494196703154086316062123787934777520599894745147260327060174336101658295022275013051816321617046927321006322752178354002696596328204277122466231388232487691224076847557856202947748540263791767128195927179588238799470987669558119422552470505956858217654904628177286026365989987106877656917
E = 65537


Welcome to HackyHolidays! Your Supersecret flag is 176955087574615470063741472647197409875117482285309340581271852382710990213049325727125711804231234813146490233229473679126800639397642380073858980601348297248196895714845780751708931869367483971257602632592317987276609144131149239628356913355893753937582033295526684103570648143766629320982809943886265840131929175495923219383837739522744946987913271495217642469261483099144404131616847257182856944641353523297845726161862062019653065904612865722942649827600090466968124488518262272506900322544403300651512798674316560281124899873116026534973842919190849918357740307152880452169695889599662477611952919511642717417

Everything indicates that the AI has encrypted the message using RSA (Rivest, Shamir, & Adleman (public key encryption technology)). (in addition to the hint in the challenge title)

Most of the RSA vulnerabilities have been due to poor implementation of the protocol by software designers.
One of the best known vulnerabilities is the Factorisation attack. (If attacker will able to know P and Q using N, then he could find out value of private key)

Let’s test to see if the AI made the same implementation mistake. For this, we use factorDB that will allow us to obtain (if they exist) the primes of a number

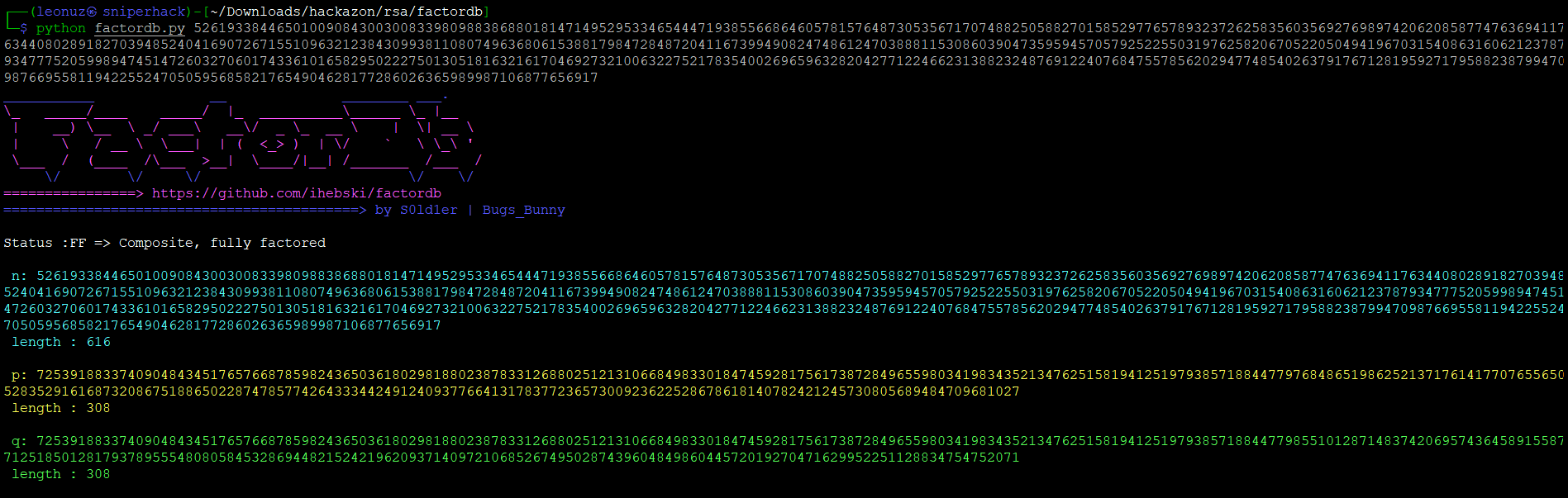
Bingo! We have found that N is fully factored, so we know p and q. With these values we will determine a totiem function named phi(n) and of course d (the private key) which will give us access to the message encrypted by the AI.

Decryption Process

We use python to help us get the rest of the values needed to decipher the message.

┌──(leonuz㉿sniperhack)-[~/Downloads/hackazon/rsa]
└─$ cat rsa.py
from Crypto.Util.number import getPrime, inverse
import binascii

p = 72539188337409048434517657668785982436503618029818802387833126880251213106684983301847459281756173872849655980341983435213476251581941251979385718844779768486519862521371761417707655650528352916168732086751886502287478577426433344249124093776641317837723657300923622528678618140782421245730805689484709681027
q = 72539188337409048434517657668785982436503618029818802387833126880251213106684983301847459281756173872849655980341983435213476251581941251979385718844779855101287148374206957436458915587712518501281793789555480805845328694482152421962093714097210685267495028743960484986044572019270471629952251128834754752071
c = 176955087574615470063741472647197409875117482285309340581271852382710990213049325727125711804231234813146490233229473679126800639397642380073858980601348297248196895714845780751708931869367483971257602632592317987276609144131149239628356913355893753937582033295526684103570648143766629320982809943886265840131929175495923219383837739522744946987913271495217642469261483099144404131616847257182856944641353523297845726161862062019653065904612865722942649827600090466968124488518262272506900322544403300651512798674316560281124899873116026534973842919190849918357740307152880452169695889599662477611952919511642717417

n = p*q
e = 65537

phi = ( q - 1 ) * ( p - 1 )

d = inverse( e, phi )
m = pow( c, d, n )
print(m)

and when we ran the script we had the deciphered message:

┌──(leonuz㉿sniperhack)-[~/Downloads/hackazon/rsa]
└─$ python rsa.py
67084070123082083065095098114048107101110125

After several tests we realized that the AI had encoded the message in integers that can be decoded in ascii characters.

We created a list of what we thought might be printable ascii characters and made a small script in python

┌──(leonuz㉿sniperhack)-[~/Downloads/hackazon/rsa]
└─$ cat convert.py
rsa_encode = [67, 84, 70, 123, 82, 83, 65, 95, 98, 114, 48, 107, 101, 110, 125]
print("rsa_decode:   ",''.join([chr(x) for x in rsa_encode]))

First we need to iterate over the msg_encode list and convert each item, creating a new list, and them, we use the join method of the empty string to join all of the strings together

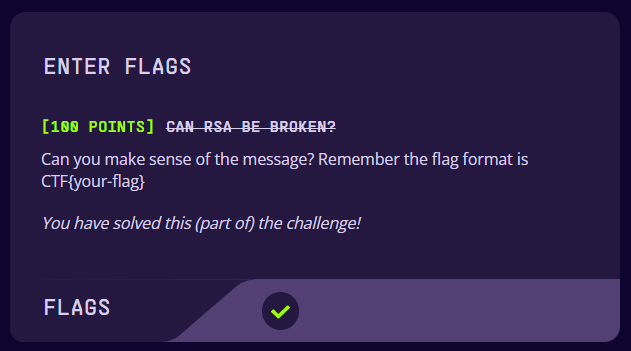
When we run the script and VOILA!!

┌──(leonuz㉿sniperhack)-[~/Downloads/hackazon/rsa]
└─$ python convert.py
rsa_decode:    CTF{RSA_br0ken}

and thus we got the encrypted message left by the IA

CTF{RSA_br0ken}

The CTF’s Way

After all it’s a CTF!!, it’s important to solve the challenges by knowing what it is all about, interacting with the different components and most importantly, Learning. That said it is also important that every CTF player has a complete arsenal of tools, and as a part of that arsenal, RsaCtfTool is one of the favorite tools among the CTF Players for solving RSA challenges. This challenge is no exception.

┌──(leonuz㉿sniperhack)-[~/Downloads/hackazon/rsa]
└─$ python RsaCtfTool/RsaCtfTool.py -n 5261933844650100908430030083398098838688018147149529533465444719385566864605781576487305356717074882505882701585297765789323726258356035692769897420620858774763694117634408028918270394852404169072671551096321238430993811080749636806153881798472848720411673994908247486124703888115308603904735959457057925225503197625820670522050494196703154086316062123787934777520599894745147260327060174336101658295022275013051816321617046927321006322752178354002696596328204277122466231388232487691224076847557856202947748540263791767128195927179588238799470987669558119422552470505956858217654904628177286026365989987106877656917 -e 65537 --uncipher 176955087574615470063741472647197409875117482285309340581271852382710990213049325727125711804231234813146490233229473679126800639397642380073858980601348297248196895714845780751708931869367483971257602632592317987276609144131149239628356913355893753937582033295526684103570648143766629320982809943886265840131929175495923219383837739522744946987913271495217642469261483099144404131616847257182856944641353523297845726161862062019653065904612865722942649827600090466968124488518262272506900322544403300651512798674316560281124899873116026534973842919190849918357740307152880452169695889599662477611952919511642717417
private argument is not set, the private key will not be displayed, even if recovered.

[*] Testing key /tmp/tmp9l8191qz.
[*] Performing fibonacci_gcd attack on /tmp/tmp9l8191qz.
100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 9999/9999 [00:00<00:00, 61322.89it/s]
[*] Performing factordb attack on /tmp/tmp9l8191qz.
[*] Attack success with factordb method !

Results for /tmp/tmp9l8191qz:

Unciphered data :
HEX : 0x0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000302165d182445d695194c33ddb6a579b93f6d
INT (big endian) : 67084070123082083065095098114048107101110125
INT (little endian) : 13791398969563348985560746647077343938117715149435991080231474109964931513438349270258949718101699149218713293706538933790089441625482047320435455289586394870840532162829549813157657448645717379923663016718650016269727880100517020602432944770560769372178838455535755463360723715988925362417695692851675556191750905690325735054097058246995323581276163500485492362262949222989335645688919986350673253321440283118074741995906942345070169928062512609219869576400006771605214575626427506598379401885104443892046343223989476686203611356584169073803136811665817216992266136331899935711599281696100177217166012569517314539520
STR : b'\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x03\x02\x16]\x18$E\xd6\x95\x19L3\xdd\xb6\xa5y\xb9?m'

If we look at the last three numbers of the “INT (big endian) value”, (125) we see that it is a printable ascii character whose value is ‘}’. If we make a list separating each character we get the following:

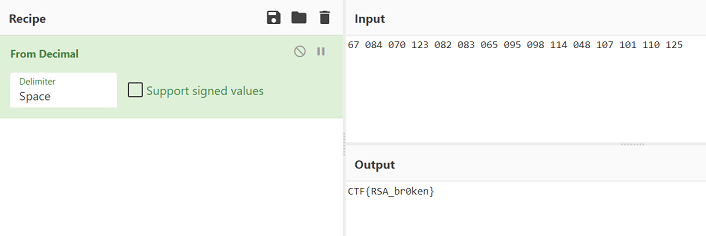
67 084 070 123 082 083 065 095 098 114 048 107 101 110 125

We take that list to CyberChef and we get the flag

Some Theory behind RSA

RSA algorithm is asymmetric cryptography algorithm. Asymmetric actually means that it works on two different keys i.e. Public Key and Private Key. As the name describes that the Public Key is given to everyone and Private key is kept private.

The idea of RSA is based on the fact that it is difficult to factorize a large integer. The public key consists of two numbers where one number is multiplication of two large prime numbers. And private key is also derived from the same two prime numbers. So if somebody can factorize the large number, the private key is compromised. Therefore encryption strength totally lies on the key size and if we double or triple the key size, the strength of encryption increases exponentially.

RSA cryptosystem

Key generation

Choose two distinct primes p and q of approximately equal size so that their product n=pq is of the required bit length. Compute ϕ(n)=(p−1)(q−1). Choose a public exponent e,1<e<ϕ(n), which is coprime to ϕ(n), that is, gcd(e,ϕ(n))=1. Compute a private exponent d that satisfies the congruence ed≡1(modϕ(n)). Make the public key (n,e) available to others. Keep the private values d, p, q, and ϕ(n) secret.

RSA Encryption scheme

Encryption rule: ciphertext, c = RsaPublic(m) = memodn, where 1<m<n−1. Decryption rule: plaintext, m = RsaPrivate(c) = cdmodn. Inverse transformation: m = RsaPrivate(RsaPublic(m)).